Closest point sparse octree for surface flow visualization
M. Kim, C.D. Hansen. “Closest point sparse octree for surface flow visualization”, 2017 IS\&T EI Visualization and Data Analysis, 2017.
Mark Kim and Charles Hansen


Abstract
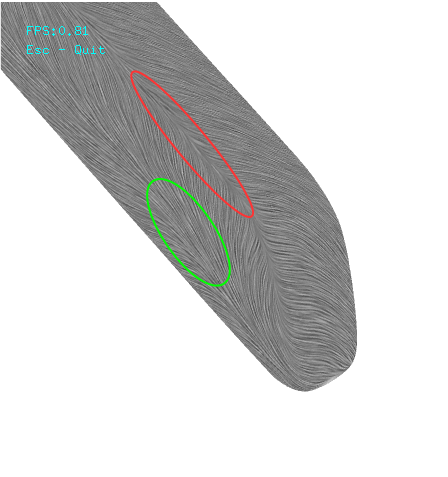
As datasets continue to increase in size and complexity, new techniques are required to visualize surface flow effectively. In this paper, we introduce a novel technique for visualizing flow on arbitrary surface meshes. This new method utilizes the closest point method (CPM), an embedding technique for solving partial differential equations (PDE) on surfaces. The CPM operates by extending values off the surface into the grid and using standard three dimensional PDE stencils to solve embedded two dimensional surface problems. To adapt unsteady flow visualization for the CPM, unsteady flow line integral convolution (UFLIC) is applied in three dimensions to the embedded surface in the grid to visualize flow on an arbitrary surface.
To address the increased size and complexity of datasets, we introduce the closest point sparse octree to efficiently represent an embedded surface. To our knowledge, this is the first sparse octree for the closest point embedding. By constructing a closest point sparse octree, complex surfaces can be represented in a memory efficient manner. Further, various techniques, such as a Laplacian filter, can be applied more easily to the embedded surface because of the CPM. Finally, the memory efficiency of our new sparse octree approach allows grids to be constructed up to $8,192^3$ in size.
Introduction
Vector field visualization is a fundamental technique in scientific visualization and important in numerous scientific and engineering fields such as computational fluid dynamics. Line Integral Convolution (LIC) is one such technique because of its simplicity and portability as well as performance on the GPU.
There are two techniques for computing LIC on surfaces: image-space methods and surface parameterization methods. Image-space methods project the visible surface geometry and velocity field into the image space and LIC is applied in the image space. By processing just the visible portions of the mesh, the computation is highly interactive due to the GPU generated LIC. However, by only processing the visible geometry, artifacts from altering the camera position can be noticed around silhouette edges or self-occluded areas of the mesh. Further, image-space based approaches cannot use other flow visualization methods such as dye advection.
In contrast to image-space techniques, a surface can be parameterized and flow visualization techniques applied in the parameter space. The state of the art in parameter space techniques utilizes the closest point embedding to apply UFLIC to surfaces. Unfortunately, this nearly-interactive scheme does not scale well as the surface requires a higher resolution grid which increases memory requirements.
In this paper we present a new method for visualizing flow on a surface. Our approach is based on the closest point method, a powerful technique for solving PDEs on embedded surfaces. Further, by using the closest point method, other partial differential equation-based flow visualization techniques, such as reaction-diffusion, can be applied to as well.
Our contributions are
- Introduce the closest point method for surface flow visualization.
- Introduce a sparse octree closest point construction technique.
- Apply unsteady flow line integral convolution (UFLIC) to the closest point method for surface flow visualization.
To perform the surface flow visualization, a sparse closest point embedding is constructed by converting the triangular mesh into a sparse three-dimensional closest point octree. Then, unsteady flow line integral convolution, or UFLIC, carries a noise field through the three-dimensional sparse closest point grid by extending the values off the surface into a surrounding grid and applying UFLIC in three dimensions.