Finite Volume WENO oscillation indicators part 4

My previous post was incorrect about the oscillation indicator matrix:

\[\begin{matrix} 1 & 0 & 0.25 \\ 0 & 4.333 & 0 \\ 0.25 & 0 & 3.11250 \end{matrix}\]

because I start with

f = x

which isn’t correct because it should be

f = x**0

instead of

f = x**1

The correct oscillation indicator matrix (when starting from \(x^0\)) is:

\[\begin{matrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 4.33333 \end{matrix}\]

Using the corrected oscillation indicator matrix, we can recreate the plot from the Garch et al. paper:

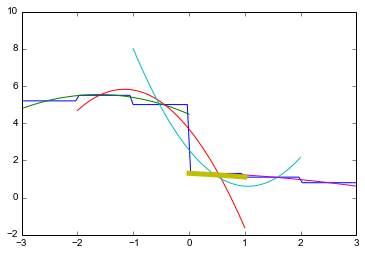
Creative Image

phi = np.array([5.2, 5.5, 5, 1.3,1.1,0.8])

w = []
w.append(Linv.dot(phi[0:3]))
w.append(Linv.dot(phi[1:4]))
w.append(Linv.dot(phi[2:5]))
w.append(Linv.dot(phi[3:6]))
w.append(Linv.dot(np.array([phi[4], phi[5], phi[5]])))

print w

sigma_l = []
epsilon = 1e-6

print len(w)
for i in range(len(w)):
    tmp = w[i].dot( Sigma)
    sigma_l.append(tmp.dot(w[i]))

print sigma_l

def fun_omega(k, i):
    if ( i == 0):
        return 1e3/(epsilon + sigma_l[k +i ])**4
    else:   
        return 1/(epsilon + sigma_l[k + i])**4
    
def fun_omega_denom(k):
    tot = 0.0
    
    for i in range(-1,2):
        tot = tot + fun_omega(k, i)
    return tot


def fun_phi(idx, x):
    tot = 0.0
    for i in range(3):
        tot = tot + w[idx][i] * x**(i)
    return tot

def fun_phi_weno(idx, x):
    tot = 0.0
    omega_tilde_j = fun_omega_denom(idx)
    
    for i in range(-1,2):
        tot = tot + fun_phi(idx+i,x) * fun_omega(idx, i) / omega_tilde_j

    return tot

xplot = np.linspace(-3, 3, 100)

vfun_phi_weno = np.vectorize(fun_phi_weno)
vfun_phi = np.vectorize(fun_phi)

y = vfun(xplot)
plt.plot(xplot,y)


xplot = np.linspace(-3,0,100)
phi_y = vfun_phi(0, np.linspace(-1,2,100))
plt.plot(xplot, phi_y)

xplot = np.linspace(-2,1,100)
phi_y = vfun_phi(1, np.linspace(-1,2,100))
plt.plot(xplot, phi_y)

xplot = np.linspace(-1,2,100)
phi_y = vfun_phi(2, xplot)
plt.plot(xplot,phi_y)


xplot = np.linspace(0,3,100)
phi_y = vfun_phi(3, np.linspace(-1,2,100))
plt.plot(xplot, phi_y)


weno_y =  vfun_phi_weno(2, np.linspace(-0.5,0.5,100))
plt.plot(np.linspace(0,1,100), weno_y, linewidth=5)

And the proper integration is:

\[0.5 \left(\left. \frac{d}{d x} 1 \right|_{\substack{ x=-0.5 }}\right)^{2} + 0.5 \left(\left. \frac{d}{d x} 1 \right|_{\substack{ x=0.5 }}\right)^{2} + 0.5 \left(\left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=-0.5 }}\right)^{2} + 0.5 \left(\left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=0.5 }}\right)^{2} = 0\] \[0.5 \left. \frac{d}{d x} 1 \right|_{\substack{ x=-0.5 }} + 0.5 \left. \frac{d}{d x} 1 \right|_{\substack{ x=0.5 }} - \left. \frac{d}{d x} x \right|_{\substack{ x=-0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=-0.5 }} + \left. \frac{d}{d x} x \right|_{\substack{ x=0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=0.5 }} = 0\] \[- 0.25 \left. \frac{d}{d x} 1 \right|_{\substack{ x=-0.5 }} + 0.25 \left. \frac{d}{d x} 1 \right|_{\substack{ x=0.5 }} - \left. \frac{d}{d x} x^{2} \right|_{\substack{ x=-0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=-0.5 }} + \left. \frac{d}{d x} x^{2} \right|_{\substack{ x=0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=0.5 }} = 0\] \[0.5 \left. \frac{d}{d x} 1 \right|_{\substack{ x=-0.5 }} + 0.5 \left. \frac{d}{d x} 1 \right|_{\substack{ x=0.5 }} - \left. \frac{d}{d x} x \right|_{\substack{ x=-0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=-0.5 }} + \left. \frac{d}{d x} x \right|_{\substack{ x=0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=0.5 }} = 0\] \[\int_{-0.5}^{0.5} \left(\frac{d}{d x} x\right)^{2}\, dx + \int_{-0.5}^{0.5} \left(\frac{d^{2}}{d x^{2}} x\right)^{2}\, dx = 1\] \[\int_{-0.5}^{0.5} \frac{d}{d x} x \frac{d}{d x} x^{2}\, dx + \int_{-0.5}^{0.5} \frac{d^{2}}{d x^{2}} x \frac{d^{2}}{d x^{2}} x^{2}\, dx = 0\] \[- 0.25 \left. \frac{d}{d x} 1 \right|_{\substack{ x=-0.5 }} + 0.25 \left. \frac{d}{d x} 1 \right|_{\substack{ x=0.5 }} - \left. \frac{d}{d x} x^{2} \right|_{\substack{ x=-0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=-0.5 }} + \left. \frac{d}{d x} x^{2} \right|_{\substack{ x=0.5 }} \left. \frac{d^{2}}{d x^{2}} 1 \right|_{\substack{ x=0.5 }} = 0\] \[\int_{-0.5}^{0.5} \frac{d}{d x} x \frac{d}{d x} x^{2}\, dx + \int_{-0.5}^{0.5} \frac{d^{2}}{d x^{2}} x \frac{d^{2}}{d x^{2}} x^{2}\, dx = 0\] \[\int_{-0.5}^{0.5} \left(\frac{d}{d x} x^{2}\right)^{2}\, dx + \int_{-0.5}^{0.5} \left(\frac{d^{2}}{d x^{2}} x^{2}\right)^{2}\, dx = 4.33333\]

Mark Kim